Compute z translate for fullscreen image at any ratio

[Yinameah]

Hello everybody,

I'm fairly new to isadora, and I'm having a lot of fun with this new tool. But I cannot understand how 3D projection is dealing with distance.

For context, I have numerous little screens with various resolutions (the scenery I'm projecting onto is a wall of frames), and I want to use 3d projection to do 3d spinning effects. Sofar so good.

But my problem is to compute the required z translate for a video to make the video stream fullscreen. I want to compute it from input ratio because I have more than 30 frames with almost as many ratios and fine tuning by hand is gonna be a pain.

I've read this, which is closely related : https://community.troikatronix... but I'm not really satisfied with the answer... I mean, all the context is great, but it doesn't seem to me that the image is rendered on a cardboard of 1.000 x 1.777 Units for a 16:9 stream. Or if so, I suck at math much worse than I thought. (this is the best explaination I could find about the math https://gamedev.stackexchange....)

Anyway, I have another problem that fried my brain even more : If I use a 3D projector or a normal projector with 3D mode enable, different z translate values are required to make the image appear the same size. So I tried many resolution, manually changing z translate to fit and many calculations to try to "reverse ingeneering" but I cannot make sense of theses values at all.

So, basically, can somebody explain what's the units we are dealing with here ? When the image is rendered in 3D space, what "real" size is given to the frame ? Or if it's really that the width is always 1.000 unit as @mark suggests in his answer, can anybody give me the math to compute this -2.75 from a 16:9 ratio (or around -1.56 if 3D projector is used)

Here is my patch where I try to figure this out. Basically, I would like the JavaScript box to output the z translate value.

This has been bugging my brain for the last 3 nights, so any help would be really, really appreciated ;-)

[and happy to be part of the isadora gang now]

[jfg]

@yinameah said:

 I am not sure to really understand. do you mean something like that:

 3d spinning effects.mov.zip

best

Jean-François 

[Woland]

@yinameah said:

I have another problem that fried my brain even more : If I use a 3D projector or a normal projector with 3D mode enable, different z translate values are required to make the image appear the same size. So I tried many resolution, manually changing z translate to fit and many calculations to try to "reverse ingeneering" but I cannot make sense of theses values at all.

 Yeah, mixing 3D Projector actors and normal Projector actors with 3D mode enabled is a headache. Try to stick to just using one or the other. I suggest trying out 3D Quad Distort and 3D Rect Project actors, as these can offer a more flexible way to work with 3D images than the 3D Projector actor.

In terms of getting an idea of how they work in relation to each other, keep in mind that some have different z translate ranges than others.

The 3D Projector and 3D Quad Distort actors have a z translate range of -100 to 100

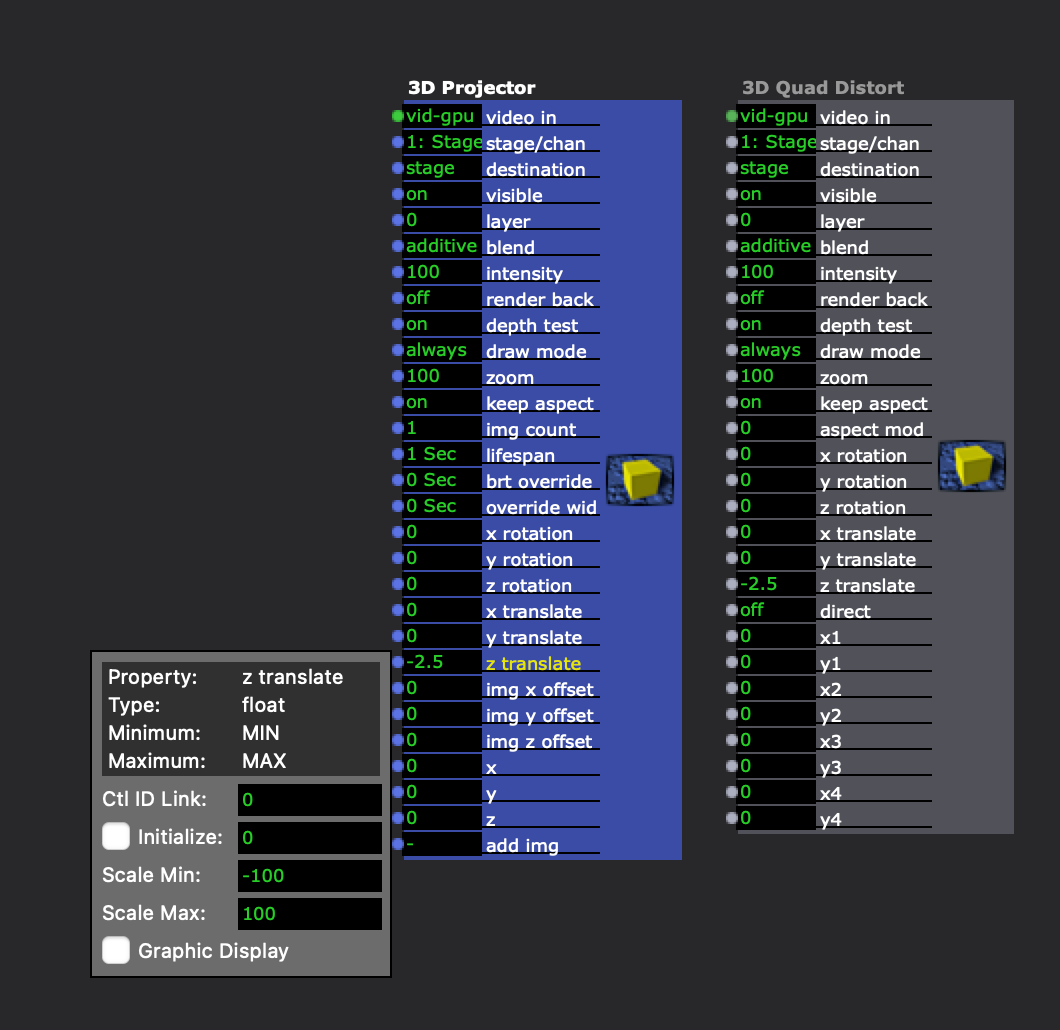
The 3D Rect Project actor has a z translate range of -200 to 200

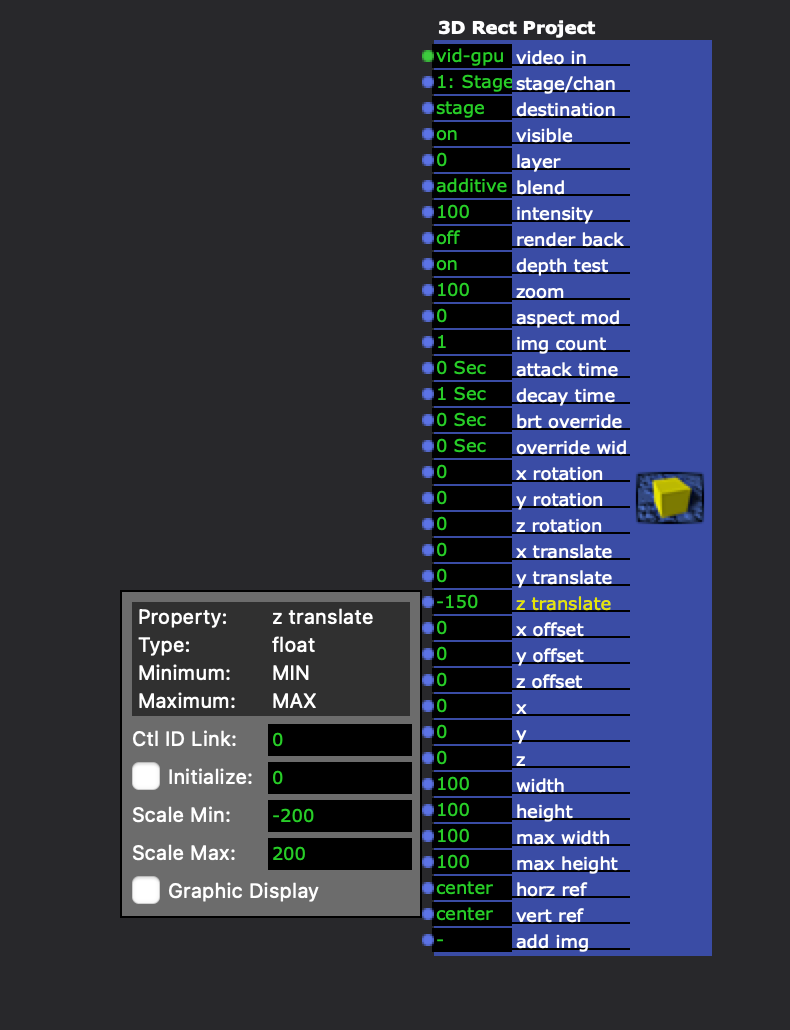
And by default, a regular Projector actor with 3D enabled doesn't have a range set for the translate z input

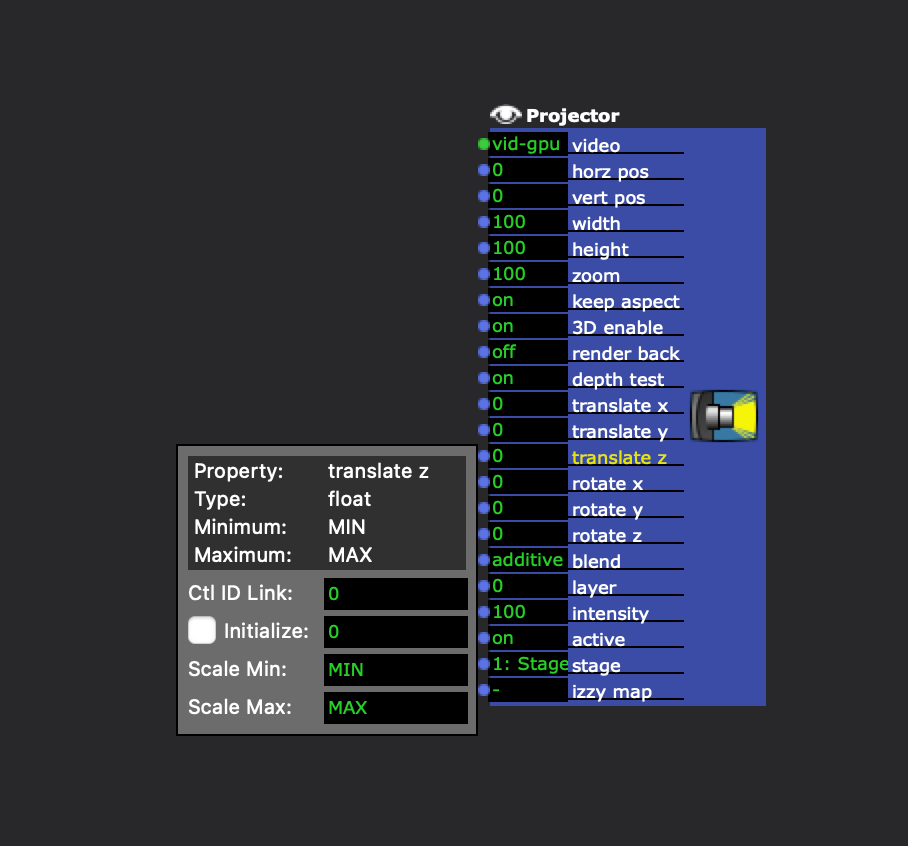
If you want the output of a 3D Projector to match the size of a regular Projector with 3D enabled, I found that multiplying the value sent to the 3D Projector by 1.77515 will cause their outputs to match in size. No idea about the math behind it, I just brute-forced it.

[jfg]

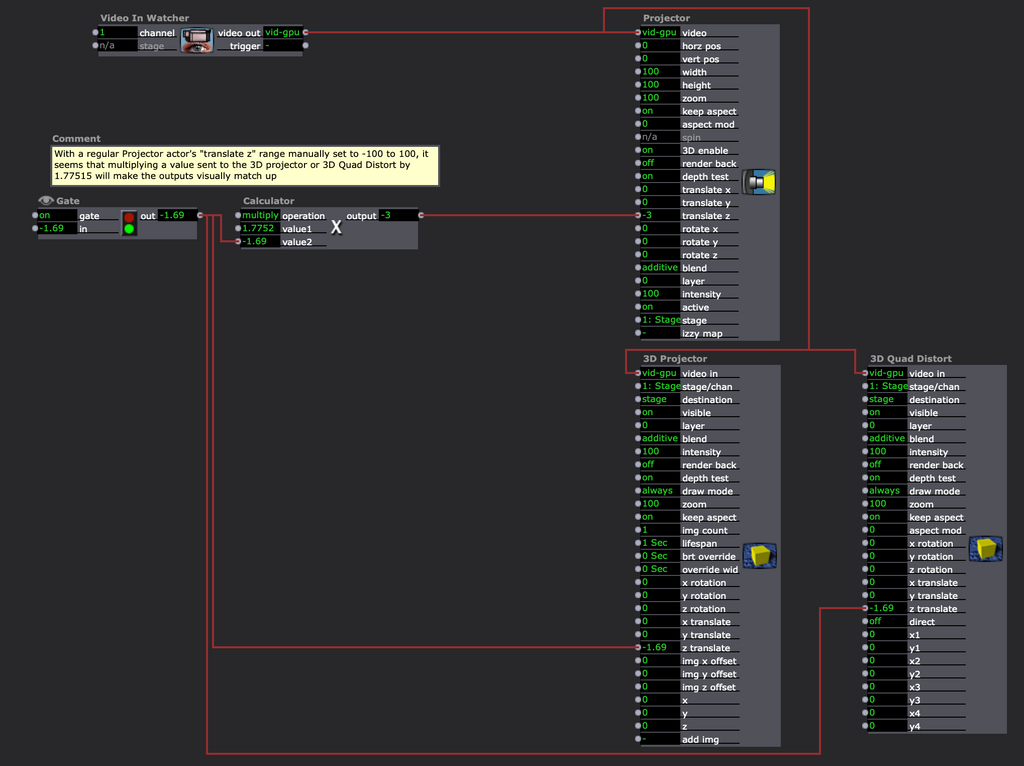
Forget what I wrote before. I deleted it. 

I still do not understand why but if the output is 16:9 all the picture/video with this ratio could be play full screen in the 3D projector with z translate set to -1,53. all other pictures/video I tried (320x240, 80x120, 120x360, 900x1300) need a z translate set to -2,03.

So I made something like that:

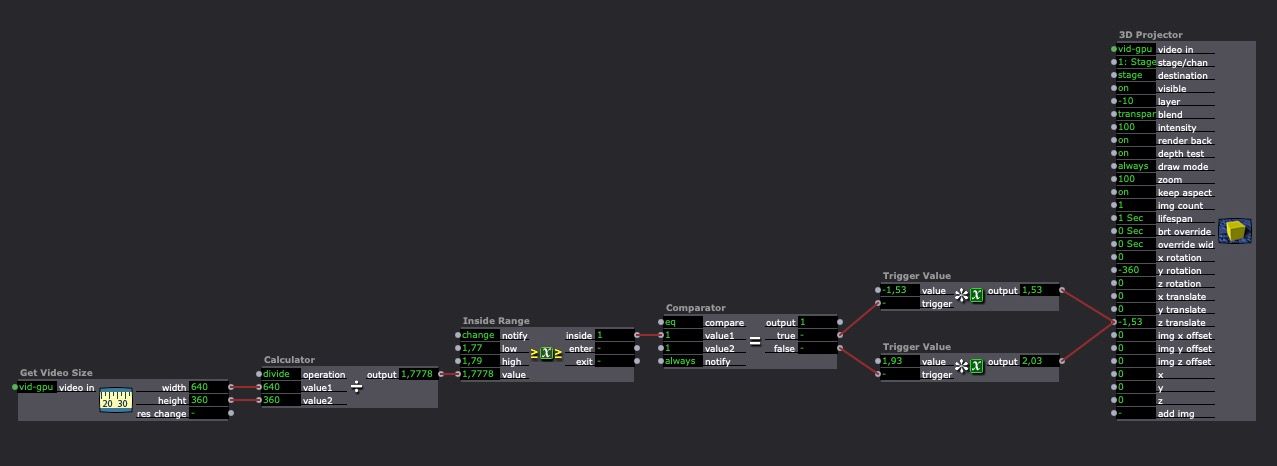
https://www.dropbox.com/s/t2na...

best

Jean-François

[Yinameah]

Thanks for your answers guys. The math is indeed a bit odd. Since I have 33 projections surfaces which all have differents ratios, I can tell that the z translate value is "ratio dependant", but it is still unclear in which ways. And it clearly depend of the 3D projector style.

In the mean time, I progressed quite a bit. Here is what I came up with, as a reference and in the hope it might help others :

- First, I ended up using 3D rect project because it was more suited for the tilting effect I was trying to achieve. (you can easily change the horizontal and vertical reference, which allows to rotate around the border of the image)

- As the 3D rect is more of a 3D square (doesn't respect the texture ratio by default), the ratio has to be adapted afterwards. And this is a really strange input range. In case, the javascript function that does the ttrick :

function main()
{
    var x = arguments[0] // Size in px of input stream
    var y = arguments[1] // Size in px of output stream

    // The output goes in "aspect mod" of 3D Rect projector

    if (x < y){
        return -100 * ( y/x ) +100
    }else if (x > y) {
        return 100 * ( x/y ) -100
    }else {
        return 0
    }
}   

- For the Z values, I brute forced it also, with something like that (It's inside a user actor, which I have 33 instances of, so each get his own little z value)

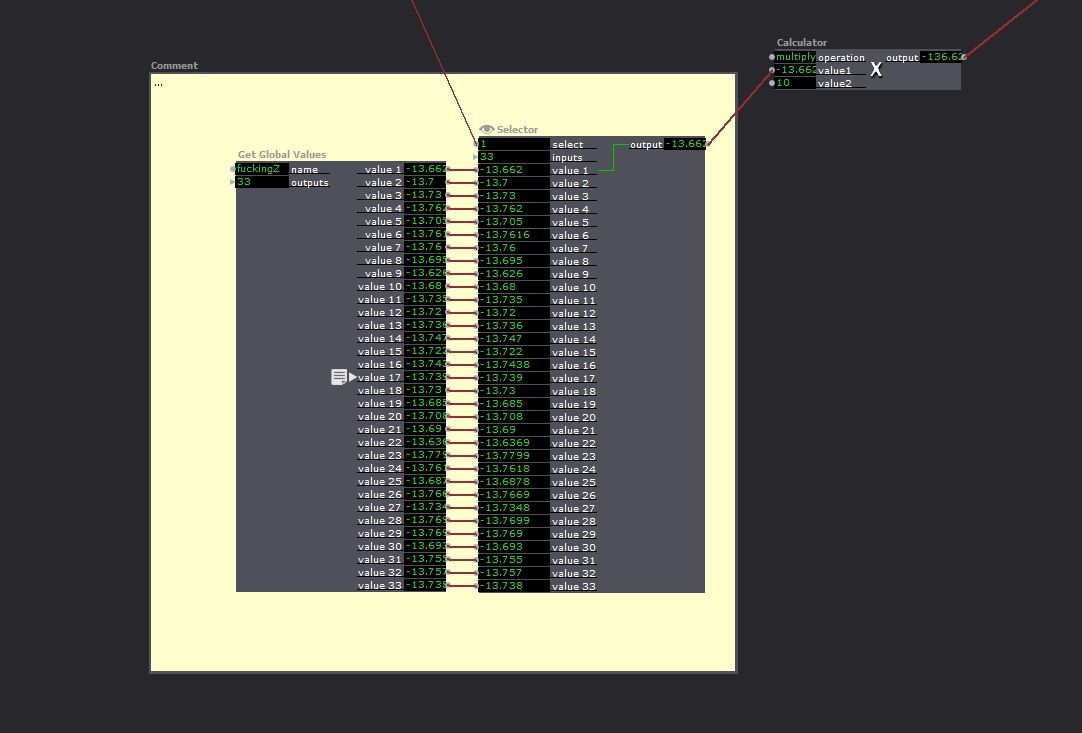
For the brute forcing itself, I did this : (this is quite a mess, but basically I generate two background colors with one pixel of difference, I send it to the corresponding virtual stage. Then the virtual stage is grabbed, and displayed on the "preview stage" with a normal projector. This way I can see clearly when the yellow border touches the blue border, and using a midi controller (with a few knob, each doing a different factor 10 increment) I managed to achieve excellent precision quite smoothly.

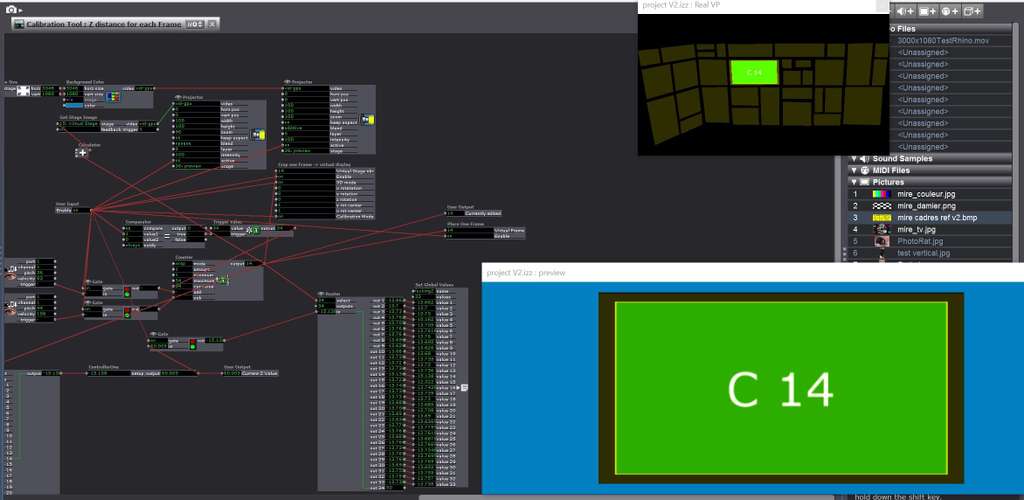
- So, quite a mess I have to say. A "match stage target size" actor that would have been nice, clearly. But each of the 33 virtual stage is re-projected on the main stage (called Real VP here) using a similar mechanism and a 3D Quad Distort projector to match then angle of the scenery (the scenery is 33 actual frames) so at the end I was able to re-use 80% of my calibration mechanism" for this other purpose, so it was less of a waste of time than I originally belived.

On the bright side, the result is pretty cool ...